Geometria e Topologia
Essa parte da exposição aborda conceitos básicos de dimensão, topologia e espaços não-euclidianos, além de investigar as variedades tridimensionais. Isso é mostrado através de filmes didáticos.
Dimensão
O primeiro vídeo começa por explicar o conceito de dimensão. Para ilustrar essa noção, usamos três categorias de objetos que tem a sua equivalência em todas as dimensões: bolas, simplexos, e cubos.
Apresentamos esses conceitos através de uma animação, que mostra simultaneamente uma bola em cada uma dessas quatro dimensões, depois um simplexo em cada uma dessas dimensões, e finalmente um cubo em cada uma dessas dimensões.
Usamos esse desenvolvimento progressivamente, a fim de ilustrar o princípio construtivo, por exemplo, partindo de um cubo de uma certa dimensão para a próxima dimensão (vide figura abaixo).

Apresentamos esses conceitos através de uma animação, que mostra simultaneamente uma bola em cada uma dessas quatro dimensões, depois um simplexo em cada uma dessas dimensões, e finalmente um cubo em cada uma dessas dimensões.
Usamos esse desenvolvimento progressivamente, a fim de ilustrar o princípio construtivo, por exemplo, partindo de um cubo de uma certa dimensão para a próxima dimensão (vide figura abaixo).
Variedades
O segundo e o terceiro vídeos (ver próxima figura) mostram exemplos simples de "variedades", que não são o espaço Euclidiano. Estas correspondem ao toro, ao bi-toro, que é um exemplo de espaço hiperbólico, e a esfera (em dimensão 1, 2 e 3).
No caso do toro, a construção é bastante simples. O 1-toro, que é um círculo, é obtido através da colagem dos pontos iniciais e finais de um segmento. O 2-toro, que é um "donut", é obtido por colagem de lados opostos de um quadrado preenchido. O 3-toro é obtido pela colagem das faces opostas de um cubo cheio. Tal construção é a primeira parte do vídeo, depois temos construções correspondentes para o espaço hiperbólico (bi-toro) e para a esfera.
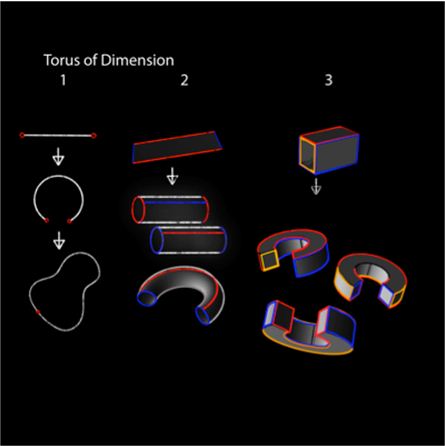
No caso do toro, a construção é bastante simples. O 1-toro, que é um círculo, é obtido através da colagem dos pontos iniciais e finais de um segmento. O 2-toro, que é um "donut", é obtido por colagem de lados opostos de um quadrado preenchido. O 3-toro é obtido pela colagem das faces opostas de um cubo cheio. Tal construção é a primeira parte do vídeo, depois temos construções correspondentes para o espaço hiperbólico (bi-toro) e para a esfera.
Visão Interior em Variedades de Dimensão 3
O quarto vídeo ilustra a visão interior em uma variedade de dimensão 3 e mostra o domínio fundamental da variedade. Para esse fim, são utilizados dois exemplos de variedades: um Toro de dimensão 3 e Cubo formado por espelhos.




