• Prova de Planetário
• Prova Individual
• Prova em Grupo
• Prova em Grupo ( Soluções )

• Prova de Planetário

Pautas de la prueba de cielo en el Planetario de Montevideo.

Consideraciones generales:

Se realizará la prueba de reconocimiento de cielo en el Planetario, en el siguiente orden de latitudes: +20°, 0°, -20° y -35°.

Las pruebas se irán desarrollando por parejas, esto es, entrarán a la sala dos concursantes a la vez, a quienes de examinará por separado pero simultáneamente, por dos equipos examinadores, y con preguntas diferentes.

Los concursantes estarán esperando en una sala anexa a la sala principal, debidamente oscurecida para que estén adecuadamente acostumbrados a la penumbra. A tales efectos, monitores del Comité Organizador Local guiarán a los concursantes, de acuerdo a cada horario.

Características de la prueba: Se le efectuará a cada concursante un conjunto de 3 preguntas, estimándose que puedan ser contestadas en unos 5 minutos. Las preguntas serán:

1) Constelación: se le pedirá al concursante la señale en el cielo del Planetario una constelación determinada. En esta pregunta, se le pedirá también que señale qué elementos destacables de la constelación considera importantes (estrellas, asterismos, etc.). Esta es la única pregunta que tiene la posibilidad de un pequeño desarrollo abierto por parte del concursante.

2) Estrella: se le pedirá al concursante que señale una estrella notable.

3) Asterismo: se le pedirá al concursante que señale en el cielo un asterismo determinado.

En todos los casos se preguntará sobre constelaciones presentes a lo largo de la noche del 11 al 12 de Octubre de 2014. A los efectos de disponer de un conjunto variado de constelaciones se ajustará el cielo de cada latitud de acuerdo al siguiente detalle (no se especifica la hora, pues puede variar de acuerdo a la disposición legal de cada país):

Latitud +20°: Se ajustará el cielo de modo que, mirando el horizonte WNE, estén presentes a la vez las constelaciones de el Cisne, Cassiopea, Osa Menor y Orión.

Latitud 0°: El cielo estará ajustado de modo que, mirando hacia el horizonte WNE,estén presentes a la vez las constelaciones de Pegaso y Orión.

Latitud -20°: Se ajustará el cielo de modo que, mirando hacia el horizonte WNE, estén presentes a la vez las constelaciones de Pegaso y Orión.

Latitud -35°: El cielo estará ajustado de modo que, mirando hacia el horizonte WNE,estén presentes a la vez las constelaciones de Pegaso y Orión.

• Prova Individual
VI OLIMPIADA LATINOAMERICANA DE ASTRONOMIA Y ASTRONAUTICA

Uruguay 2014

PRUEBA INDIVIDUAL

PROBLEMA I

La densidad de cráteres (o sea, número de cráteres por unidad de ´area) en una superficie planetaria o en un satélite natural nos puede brindar información sobre la edad de formación de la superficie, especialmente si no hay procesos de erosión que borren los registros de impactos, pues las superficies más craterizadas serán ma´s antiguas que las menos craterizadas. Analizando la superficie de un satélite natural de un planeta en el Sistema Solar se encuentra que existe una región A de 900.000 km2 de área con 3200 cráteres de radio mayor o igual a 100 metros. También se encuentra que existe otra regio´n B con un área de 1.200.000 km2 conteniendo 2000 cráteres de radio mayor o igual a 100 metros.

1) (4 puntos) Asumiendo que el flujo de proyectiles fue el mismo en toda la superficie del satélite y que ha sido constante con el transcurso del tiempo calcule la edad de la superficie A en relación a la de B.

a 1.33
b 1.20
c 2.66
d 1.60
e 2.13 *

PROBLEMA II

La siguiente función

N (R) = 2 × 106 × R−2.5

permite estimar la cantidad N de asteroides con radio mayor o igual a R kilómetros en el cinturón principal, donde R debe expresarse en km.

1) (3 puntos) Utilice la funci´on para calcular el nu´mero de asteroides con radio mayor o igual a 10 km en el cinturón principal.

a 2336
b 6325000
c 2000000
d 21456
e 6325 *

PROBLEMA III

Asumiendo que la luminosidad del Sol es L = 3.8 × 1026

W y sabiendo que la fuente de energía proviene de la transformacio´n de masa en energía dada por la ecuación E = mc2

1) (3 puntos) Calcular cuántos kilogramos por segundo se transforman en energía en el Sol.

a 4.2 × 1015 kg/s
b 2.2 × 109 kg/s
c 4.2 × 109 kg/s *
d 2.2 × 1015 kg/s
e 3.2 × 106 kg/s

2) (4 puntos) Calcular la energía por segundo y por metro cuadrado que llega a la Tierra.

a 1.8 × 109 J/m2
b 1.4 × 103 J/m2
c 1.3 × 106 W/m2
d 1.3 × 103 W/m2 *
e 1.8 × 103 W/m2

• Prova em Grupo

VI OLIMPIADA LATINOAMERICANA DE ASTRONOMIA Y ASTRONAUTICA
Lavalleja - Uruguay, 10 al 16 de octubre de 2014

PRUEBA TEORICA GRUPAL

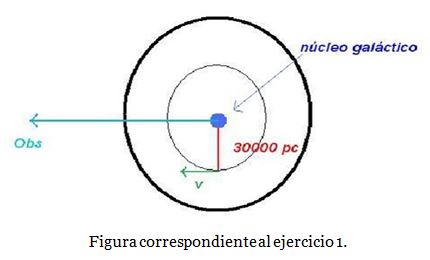
1. Para una cierta galaxia espiral se estima una masa visible de 1011 masas solares. Se procede a observar con un radiotelescopio la línea de 21 cm proveniente de una nube de hidrógeno neutro ubicada en el plano medio de la galaxia a una distancia de 30000 parsecs del centro de la galaxia (ver figura 1). Para la línea se observa un corrimiento por efecto Doppler de 1, 54 × 10−4 m. Se sabe además que la visual al observador está prácticamente contenida en el plano medio de la galaxia. Se pide calcular:

(a) (3 puntos) la velocidad de rotación de la nube de hidrógeno en base al corrimiento Doppler medido en la línea de 21 cm, asumiendo que la nube es una masa puntual que gira en torno al centro galáctico en una órbita circular;
(b) (4 puntos) la velocidad de rotación teórica que debería tener la nube de hidrógeno si toda la masa visible de la galaxia estuviera concentrada en su centro;
(c) (4 puntos) si hubiese alguna diferencia entre la velocidad de rotación teórica calculada en (b) con la medida en (a), ¿cuál sería la causa m´as importante de esa diferencia?. Fundamente su respuesta.



2. La figura muestra la curva de luz de una binaria eclipsante tipo Algol, cuyo plano orbital yace en la dirección de la visual. Se indican las magnitudes aparentes mA y mB , correspondientes a los mÍnimos primario y secundario de la curva de luz, respectivamente. La profundidad de cada mínimo ∆mag se define como la diferencia entre la magnitud total de la binaria mtot (cuando no hay eclipse) y la magnitud mA o mB . Sean TB y TA las temperaturas efectivas de la componente más brillante y de la componente más débil, respectivamente. Las dos componentes tienen el mismo radio R.



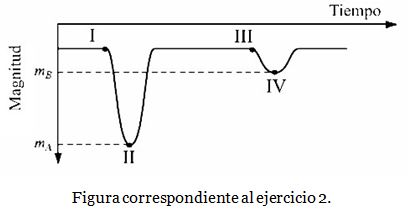
(a) (3 puntos) Realice un esquema de la posición relativa entre las dos componentes del sistema, con respecto al observador, correspon- dientes a los siguientes puntos de la curva de luz: I) antes que comience el decaimiento hacia el mínimo primario, II) cuando se alcanza el mínimo primario, III) antes que comience el decaimiento hacia el mínimo secundario, IV) cuando se alcanza el mínimo secundario. Indique claramente cual es la componente A y cual es la B.
(b) (4 puntos) Encuentre una expresión que relacione la profundidad de cada mínimo de la curva de luz con la luminosidad total de la binaria (Ltot) y la luminosidad individual de cada componente (LA, LB ).
(c) (4 puntos) Sabiendo que las temperaturas efectivas de las componentes son TB = 12000 K y TA = 5000 K, calcule la profundidad ∆mag de cada mínimo.

3. Si toda la masa de la Luna la distribuyeramos por la superficie terrestre preservando la densidad lunar;
(a) (4 puntos) ¿en cuánto aumentar´ıa el radio de esta nueva versión del planeta Tierra?
(b) (4 puntos) Siendo g y g′ las aceleraciones de la gravedad en la superficie, antes y después de la incorporación de la masa, respectivamente, calcule el cociente g′/g.
Datos: RL = 1740 km, RT = 6370 km, ML = 0.012MT .

4. El período orbital de un asteroide es exactamente la tercera parte del per´ıodo orbital de Júpiter, siendo éste de 11.87 an˜os.
(a) (3 puntos) Calcule el semieje mayor a de la órbita del asteroide.
(b) (4 puntos) Sabiendo que la órbita del asteroide tiene excentricidad e = 0.3, y que es coplanar con la eclíptica, calcule la mínima distancia posible a la que este asteroide puede acercarse a la Tierra, suponiendo que la órbita de la Tierra sea circular.
5. La llamada “Ley de Hubble” es una relación empírica que permite estimar la distancia a los objetos más remotos del Universo. Dicha relación establece que la velocidad de recesión v de las galaxias lejanas es directamente proporcional a su distancia r . A su vez, cuando v << c, puede determinarse v a partir del corrimiento Doppler de las l´ıneas espectrales z dado que z = v/c, siendo c la velocidad de la luz en el vac´ıo.
(a) (4 puntos) Suponiendo que la constante de Hubble H0 = 65 km s−1 Mpc−1, ¿a qué distancia se encuentra una galaxia con z = 0.05?

(b) (4 puntos) Suponiendo que las velocidades han permanecido constantes en el tiempo, ¿cuánto tiempo le ha tomado a una galaxia remota cualquiera alcanzar su distancia actual de nosotros, según el modelo cosmológico est´andar del Big Bang? Considere c = 3.0 × 108 m s−1 . 1 pc = 30.8 ×1012 km.

6. Se descubre un planeta extrasolar orbitando alrededor de una estrella a 25 pc de distancia del Sol con el telescopio Gemini Sur de 8.1 m en λ = 1.6 × 10−6 m. El exoplaneta está a 5 ua de la estrella y ésta tiene una masa de 1.1 M⊙.

(a) (3 puntos) Estime la velocidad orbital del planeta asumiendo una órbita circular.
(b) (4 puntos) Estime cuantos meses tendrían que esperar los astrónomos para observar el planeta moverse en su órbita. Nota: Esto ocurre aproximadamente cuando el planeta avanza una distancia equiv- alente al poder de resolución del telescopio.

7. Haga un esquema de las posiciones relativas de la Tierra, el Sol y la Luna, y los conos de sombra y de penumbra, durante:
(a) (3 puntos) un eclipse total de Sol. Indique cualitativamente la zona de la Tierra desde donde se vería el eclipse total, y la zona desde donde se vería el eclipse parcial;
(b) (3 puntos) un eclipse anular de Sol. Indique cualitativamente la zona de la Tierra desde donde se vería el eclipse anular, y la zona desde donde se vería el eclipse parcial.

• Prova em Grupo (Soluções)

VI OLIMPIADA LATINOAMERICANA DE ASTRONOMIA Y ASTRONAUTICA
Lavalleja - Uruguay, 10 al 16 de octubre de 2014
SOLUCIONES - PRUEBA TEORICA GRUPAL


2. (a)